AutoEncoder by Forest: ランダムフォレストをオートエンコーダとして使う

09 January 2018

この前のShibuya.lispの懇親会で教えてもらった論文(AutoEncoder by Forest)を読んだのでcl-random-forest (解説記事)で再現してみた。どうやらDeepForestの研究グループらしい。

どのような内容なのか一言でいうと、入力データがランダムフォレストの各決定木のどの葉ノードに入るかが分かれば、元の入力を再構成できるという話だった。つまり、エンコードは入力データから各決定木の葉ノードのインデックスを調べ、そのベクトルを出力することに対応する。逆にデコードは葉ノードから根ノードへ逆に辿っていき、入力の範囲を制限していき、最後にそこから代表値を選ぶことに対応する。エンコーダの訓練は通常のランダムフォレストでモデルを作るだけなので、GPUを使ったニューラルネットのオートエンコーダよりも100倍速いと主張されている。(なおデコード速度では負けている模様)

決定木の非終端ノードには分岐に使う特徴とその閾値が保存されており、データが分岐に入ってくるとそのデータの中の対応する特徴を調べて、閾値を越えていれば左の子ノードに、そうでなければ右の子ノードへと進む。それを繰り返して葉ノードに到達したとき、その経路は入力データの範囲を制限するルールの羅列になっているはずだ。逆に、入力データがどの葉ノードに入ったかさえ分かれば、親ノードを辿っていくことで決定木からルールの羅列を得ることもできる。

さらに、決定木が複数あるときは、そのルールの羅列のANDを取ることで、より入力の範囲を絞り込める。

以下の図は上記論文のFigure1だが、n個ある決定木の葉ノードが分かれば、そこから各決定木の分岐の経路(赤い線)が一意に決まり、そこから入力の範囲を求められる。

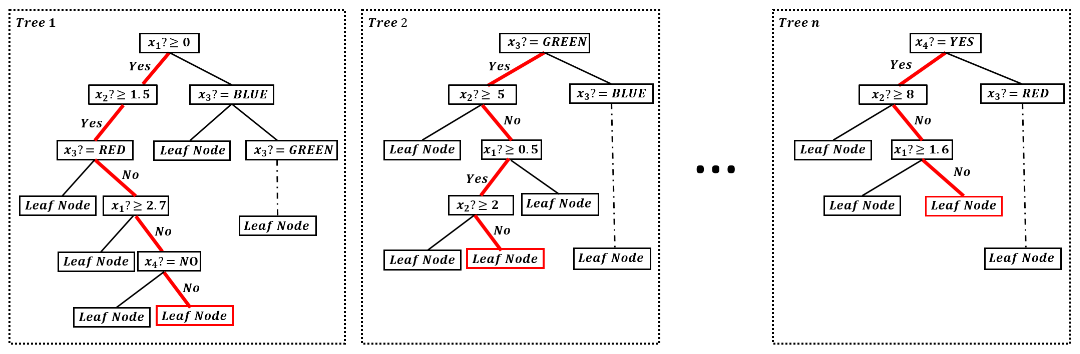
例えばx1に関する条件であれば、決定木1から 2.7 > x1 >= 0 であることが分かり、決定木2から x1 >= 0.5 であることが分かり、決定木nから x1 < 1.6 であることが分かるので、見えている範囲からだけでも 1.6 > x1 >= 0.5 の範囲にあることが分かる。この上と下の平均を取るなどして代表値を出してx1の値の復元値ということにする。

実際にやってみた

cl-random-forest/src/reconstruction.lisp

まずノードに親ノードへのリンクを新たに持たせるようにした。特徴量ごとに上限と下限の値を保存する配列を用意し、葉ノードから逆にたどりながら更新していく関数reconstruction-backwardと、さらにそれを各決定木についてやり、最後に下限と上限の平均を取って返す関数reconstruction-forestを定義する。

(defun reconstruction-backward (node input-range-array)
  (let ((parent-node (node-parent-node node)))
    (if (null parent-node)
        input-range-array
        (let ((attribute (node-test-attribute parent-node))
              (threshold (node-test-threshold parent-node)))
          (if (eq (node-left-node parent-node) node)
              (when (> threshold (aref input-range-array 0 attribute)) ; left-node
                (setf (aref input-range-array 0 attribute) threshold))
              (when (< threshold (aref input-range-array 1 attribute)) ; right-node
                (setf (aref input-range-array 1 attribute) threshold)))
          (reconstruction-backward parent-node input-range-array)))))

(defun reconstruction-forest (forest datamatrix datum-index)
  (let* ((dim (forest-datum-dim forest))
         (input-range-array (make-array (list 2 dim) :element-type 'double-float))
         (result (make-array dim :element-type 'double-float)))

    ;; initialize input-range-array
    (loop for i from 0 below dim do
      (setf (aref input-range-array 0 i) most-negative-double-float
            (aref input-range-array 1 i) most-positive-double-float))

    ;; set input-range-array for each dtree
    (dolist (dtree (forest-dtree-list forest))
      (reconstruction-backward
       (find-leaf (dtree-root dtree) datamatrix datum-index)
       input-range-array))

    ;; 片側しか抑えられていない場合はとりあえず0を入れておく
    (loop for i from 0 below dim do
      (when (= (aref input-range-array 0 i) most-negative-double-float)
        (setf (aref input-range-array 0 i) 0d0))
      (when (= (aref input-range-array 1 i) most-positive-double-float)
        (setf (aref input-range-array 1 i) 0d0)))

    (loop for i from 0 below dim do
      (setf (aref result i) (/ (+ (aref input-range-array 0 i)
                                  (aref input-range-array 1 i))
                               2d0)))
    result))

MNISTでやってみる

cl-random-forest/example/reconstruction/mnist.lisp

;; まずLIBSVMデータセットのMNISTのデータを読み込む
(defparameter mnist-dim 784)
(defparameter mnist-n-class 10)

(let ((mnist-train (clol.utils:read-data "/home/wiz/datasets/mnist.scale" mnist-dim :multiclass-p t)))
  ;; Add 1 to labels in order to form class-labels beginning from 0
  (dolist (datum mnist-train) (incf (car datum)))
  (multiple-value-bind (datamat target)
      (clol-dataset->datamatrix/target mnist-train)
    (defparameter mnist-datamatrix datamat)
    (defparameter mnist-target target)))

;; ランダムフォレストを作る
;; 親ノードを記録するオプションSAVE-PARENT-NODE?を真にしておくことに注意
(defparameter mnist-forest
  (make-forest mnist-n-class mnist-datamatrix mnist-target
               :n-tree 500 :bagging-ratio 0.1 :max-depth 15 :n-trial 28 :min-region-samples 5
               :save-parent-node? t))

;; 再構成を実行
(defparameter *reconstruction*
  (reconstruction-forest mnist-forest mnist-datamatrix 0))

;; 葉ノードのインデックスのベクトルとしてエンコード
(defparameter index-datum (encode-datum mnist-forest mnist-datamatrix 0))
;; デコード
(defparameter *reconstruction2* (decode-datum mnist-forest index-datum))

この*reconstruction*に再構成した結果が入っている。make-forestのオプションを色々変えてプロットしてみると以下のようになる。

:n-tree 100 :bagging-ratio 0.1 :max-depth 40 :n-trial 28 :min-region-samples 5
:n-tree 500 :bagging-ratio 0.1 :max-depth 15 :n-trial 28 :min-region-samples 5
:n-tree 1000 :bagging-ratio 0.1 :max-depth 30 :n-trial 28 :min-region-samples 5
:n-tree 500 :bagging-ratio 0.1 :max-depth 15 :n-trial 1 :min-region-samples 5
:n-tree 1000 :bagging-ratio 0.1 :max-depth 30 :n-trial 1 :min-region-samples 5

cl-random-forestでランダムフォレストを学習するときは、ランダムに何回か枝を分岐させてみて、情報利得(エントロピーやジニ係数の減少幅など)が最も大きいものを残す。この情報利得の計算時に教師信号が使われるのだが、逆に言えば、分岐の試行回数が1回で、完全にランダムに分岐を決める場合(completely-random tree forestsとかExtremely Randomized Treesとか呼ばれる)は教師信号はまったく使われないので教師なし学習と見なせる。

下2つは分岐の試行回数:ntrialが1回なので、completely-random tree forestと言える。再構成の精度はこちらの方が良いことが分かる。上3つは教師信号の情報を使って、正しい分類ができるように学習したランダムフォレストから再構成した画像であり、分類に必要のない情報は捨てられていることが分かる。分類上重要になる中心付近の特徴に対しては多くの分岐が割かれており、逆に周辺の真っ黒になっている部分には対応する枝の分岐が無いので上限も下限も設定されていない。

感想

実装は簡単だったし勉強になった気がする
データに対応する葉ノードのインデックスのベクトルを新たな特徴量とするという部分は前に実装したGlobal Refinement of Random Forestとまったく同じだなと思った
オートエンコーダとして役に立つかは未知数(ノイズには強いらしい)
次はDeepForestを実装する(予定)