メモ: Clojureの遅延シーケンスについて

27 December 2017

プログラミングClojureのフィボナッチ数の例

プログラミングClojureを読んでいて、遅延シーケンスの例としてフィボナッチ数が出てくるのだが、いまいち感覚が掴めなかったのでREPLでいじくりまわしてみた。

遅延シーケンスによるフィボナッチ数の定義は、

(defn lazy-seq-fib
  ([]
   (concat [0 1] (lazy-seq-fib 0N 1N)))
  ([a b]
   (let [n (+ a b)]
     (lazy-seq
      (cons n (lazy-seq-fib b n))))))

(take 10 (lazy-seq-fib))
; => (0 1 1N 2N 3N 5N 8N 13N 21N 34N)

Clojureでは同名の関数で引数の数によって振る舞いを切り換えることができる。最初の引数なしの場合が基底部分で、次の2引数の場合が帰納部分ということになる。

ランダムな無限シーケンス

ほぼ同じ構造で、帰納部分で乱数をくっつけるだけのシーケンスをつくってみる。

(defn random-seq
  ([]
   (concat [-2 -1] (random-seq 0N 1N)))
  ([a b]
   (let [n (rand 1)]
     (println "a: " a ", b: " b ", n: " n)
     (lazy-seq
      (cons n (random-seq b n))))))

(take 10 (random-seq))
; => (-2 -1 0.8592130206713182 0.7569570617739411 0.4014687684829018 0.2033552985966114 0.12564206892627539 0.6095217849824555 0.1040247746814027 0.9866658377796264 0.982991751770464 0.27706913712472747 0.39140441828392025)

帰納部分でのprintlnの印字結果は

a:  0N                   b:  1N                   n:  0.8592130206713182
a:  1N                   b:  0.8592130206713182   n:  0.7569570617739411
a:  0.8592130206713182   b:  0.7569570617739411   n:  0.4014687684829018
a:  0.7569570617739411   b:  0.4014687684829018   n:  0.2033552985966114
a:  0.4014687684829018   b:  0.2033552985966114   n:  0.12564206892627539
a:  0.2033552985966114   b:  0.12564206892627539  n:  0.6095217849824555
a:  0.12564206892627539  b:  0.6095217849824555   n:  0.1040247746814027
a:  0.6095217849824555   b:  0.1040247746814027   n:  0.9866658377796264
a:  0.1040247746814027   b:  0.9866658377796264   n:  0.982991751770464
a:  0.9866658377796264   b:  0.982991751770464    n:  0.27706913712472747
a:  0.982991751770464    b:  0.27706913712472747  n:  0.39140441828392025

aとかbにはそのシーケンスでの前の値が入っていることが分かる。フィボナッチ数では2つ前までの値を見ているので帰納部分が2引数だったというわけだ。

基底部分でのrandom-seqの返り値は帰納部分でconsしている値(n)の列であることが分かる。基底部分での引数は捨てられる、というか次回以降の計算に使われるだけで返り値には現れない。ので、便宜上concatで基底部分での値をくっつけていたというわけだ。

ということは3つ前までの値を見るなら帰納部分の引数の数を3にすればいい。

(defn random-seq3
  ([]
   (concat [-3 -2 -1] (random-seq3 0N 1N 2N)))
  ([a b c]
   (let [n (rand 1)]
     (println "a: " a ", b: " b ", c: " c ", n: " n)
     (lazy-seq
      (cons n (random-seq3 b c n))))))

(take 10 (random-seq3))
; => (-3 -2 -1 0.7207027379256533 0.8851641826010639 0.6057102914278899 0.7351487328660473 0.10841825608663269 0.8877903748856399 0.2971740991711813)

a:  0N                   b:  1N                   c:  2N                   n:  0.7207027379256533
a:  1N                   b:  2N                   c:  0.7207027379256533   n:  0.8851641826010639
a:  2N                   b:  0.7207027379256533   c:  0.8851641826010639   n:  0.6057102914278899
a:  0.7207027379256533   b:  0.8851641826010639   c:  0.6057102914278899   n:  0.7351487328660473
a:  0.8851641826010639   b:  0.6057102914278899   c:  0.7351487328660473   n:  0.10841825608663269
a:  0.6057102914278899   b:  0.7351487328660473   c:  0.10841825608663269  n:  0.8877903748856399
a:  0.7351487328660473   b:  0.10841825608663269  c:  0.8877903748856399   n:  0.2971740991711813
a:  0.10841825608663269  b:  0.8877903748856399   c:  0.2971740991711813   n:  0.03815903888726235

なるほど。

ランダムウォーク

ランダムな値をくっつけるだけだと前の値を使っていないじゃないか、ということで、シーケンスの直前の要素に0を中心とした乱数を足していくランダムウォーク列を定義してみる。

(defn random-walk
  ([]
   (cons 0.0 (random-walk 0.0)))
  ([pre]
   (let [n (+ pre (- (rand 1.0) 0.5))]
     (lazy-seq
      (cons n (random-walk n))))))

(require '[gnuplot.core :as g])

(g/raw-plot!
 [[:set :title "simple-test"]
  [:plot
   (g/list ["-" :title "path" :with :lines])]]
 [(mapv (fn [elm1 elm2] [elm1 elm2])
        (take 20000 (random-walk))
        (take 20000 (random-walk)))])

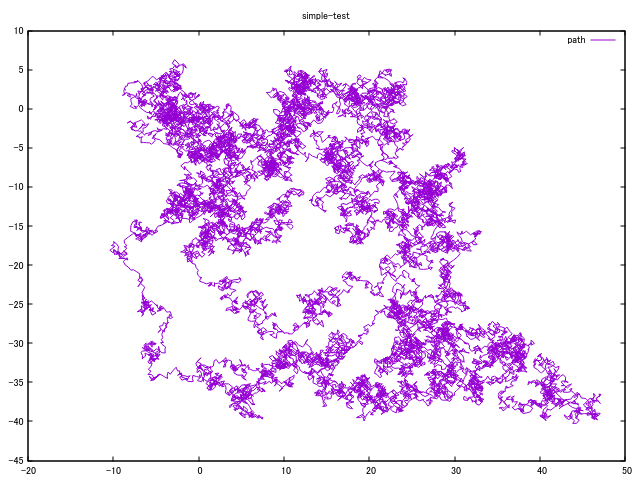
直前の位置だけではなくてその前の移動での変化量を減衰させて次の移動に影響させる、慣性みたいなものを導入してみたりできる。

(defn random-walk2
  ([]
   (concat [0.0 0.0] (random-walk2 0.0 0.0)))
  ([prepre pre]
   (let [n (+ (* 0.2 (- pre prepre))
              pre
              (* 0.8 (- (rand 1.0) 0.5)))]
     (lazy-seq
      (cons n (random-walk2 pre n))))))

N次のマルコフ連鎖なんかも綺麗に書けそうだ。

まとめ

遅延シーケンス完全に理解した！

lisp clojure 1